Non-holonomic robots, due to their constraints, require sophisticated motion planning algorithms for navigation. Ackerman steering is a geometric arrangement of linkages in the steering of a car or other vehicle designed to solve the problem of wheels on the inside and outside of a turn needing to trace out circles of different radii. Here are three different types of motion planning algorithms often used in this context:
Sampling-based planners
These incredible planners, known as Rapidly-exploring Random Trees (RRT) and Probabilistic Roadmaps (PRM), have the power to construct a magnificent graph of viable paths within the robot’s configuration space. Through tireless exploration and search within this remarkable graph, they uncover a divine path from the start to the glorious goal. These planners exhibit their prowess in navigating complex, high-dimensional configuration spaces with unfailing effectiveness. Notably, they possess the remarkable attribute of probabilistic completeness, ensuring the discovery of a solution if it exists, given ample time for their magical abilities to unfold.
Optimization-based planners
This exquisite category encompasses the illustrious technique known as Model Predictive Control (MPC), which astutely capitalizes on a model of the robot’s dynamic behavior to foresee its future states. Armed with this foresight, MPC deftly optimizes the control input, endeavoring to minimize a cost function across these envisioned states. The brilliance of MPC shines particularly bright for non-holonomic robots, as it remarkably incorporates the intricate dynamics of the robot into the very fabric of the planning process. Truly, it is a union of the art of optimization and the science of control.
Artificial Potential Fields
A magnificent approach where the robot is irresistibly drawn towards its beloved goal location, as if by an alluring potential field. Simultaneously, it is gently repelled by another potential field, ingeniously designed to shield it from perilous obstacles. The elegance of this method lies in its impeccable efficiency, as it deftly manages to preserve valuable computational resources. However, it is worth noting that this journey through potential landscapes may occasionally lead the robot astray, trapped within the clutches of local minima from which escape seems impossible.
In the case of non-holonomic robots, these methods need to be extended or modified to take the non-holonomic constraints into account. For example, the steering angle of an Ackermann steering vehicle or the speed of a differential drive robot may be limited, which imposes a constraint on the robot’s velocity.
Ackerman steering based motion planning
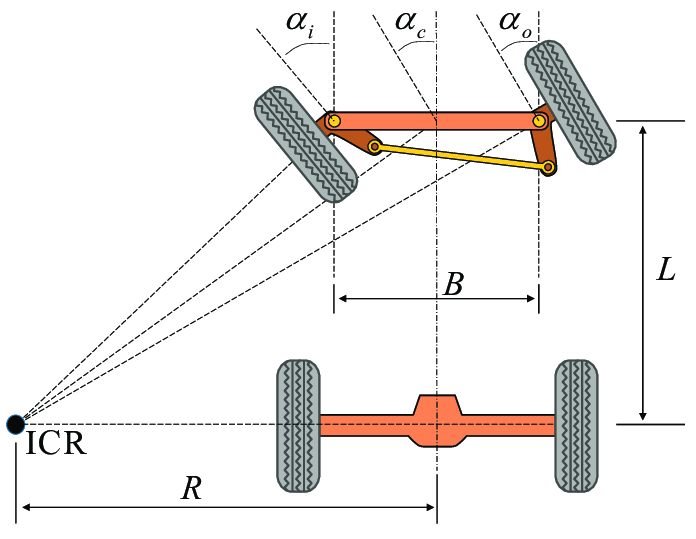
Ackerman steering is a geometric arrangement of linkages in the steering of a car or other vehicle designed to solve the problem of wheels on the inside and outside of a turn needing to trace out circles of different radii. It was invented by the German carriage builder Georg Lankensperger in Munich in 1817, then patented by his agent in England, Rudolph Ackermann (1764–1834) in 1818 for horse-drawn carriages.
In the context of motion planning, Ackerman steering is often used in the design and control of vehicles that move in a plane (e.g., cars, trucks, wheeled robots), and it’s particularly useful for vehicles that have non-holonomic constraints, meaning they can’t move in certain directions.
Ackerman steering based motion planning involves creating a model of the vehicle’s movement based on the Ackerman steering principles, and then using this model to plan a path from a start point to a goal point. This path planning takes into account the vehicle’s constraints, such as its minimum turning radius.
The motion planning algorithm would typically generate a series of steering and velocity commands to move the vehicle from the start to the goal while avoiding obstacles. This can be a complex problem, especially in dynamic environments, and may involve the use of advanced techniques such as probabilistic roadmaps, rapidly-exploring random trees (RRTs), or other methods used in robotics.
It’s important to note that the specifics of the motion planning algorithm can depend on the exact nature of the vehicle and the environment. For example, a motion planning algorithm for an autonomous car driving in an urban environment might need to take into account traffic rules, other vehicles, pedestrians, etc., while an algorithm for a wheeled robot in a warehouse might have different considerations.